- Dette emne har 7 svar og 1 stemme, og blev senest opdateret for 6 år, 2 måneder siden af Bjarne. This post has been viewed 760 times
-
Indlæg
-
Bjarne- Super Nova
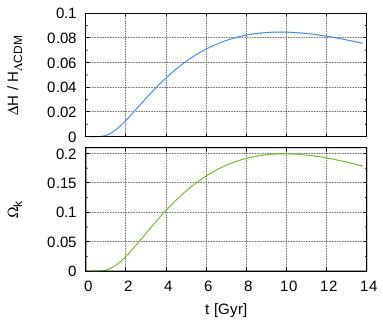Målinger af hubblekonstanten ved anvendelse af fluktuationer i den kosmiske mikrobølgebaggrundsstråling er ikke i overensstemmelse med målinger af den lokale værdi udledt ud fra afstande til supernovaer af type Ia. Det har endnu ikke været muligt at forklare forskellen ved enten systematiske observationsfejl eller ny fysik. Denne artikel fremfører en ny løsning på problemet. Den anvender en relativistisk simulering af Universets storskalastruktur kombineret med en ray-tracing algoritme. Simuleringen tager højde for en relativistisk, ikke-lineær udvikling af den kosmiske struktur, hvorunder den rumlige krumning udvikler sig fra nul i det tidlige univers til en svag negativ krumning i det nuværende univers. Dette fænomen forøger ekspansionsraten sammenlignet med en rumlig flad ΛCDM-model. (Ωk i figuren er den negative krumning).
Resultatet af ray-tracing analysen viser, at Universet, hvis det opfylder betingelserne fra Planck-satellittens målinger, bør have den nuværende hubblekonstant H0 = 72.5±2.1 km/s/Mpc. Hvis de relativistiske korrektioner ikke medtages, giver simuleringen med ray-tracing en nuværende hubblekonstant på H0 = 68.1±2.0 km/s/Mpc. Inklusionen af relativistiske effekter kan tilsyneladende forklare, hvorfor de lokale målinger giver en højere værdi end den kosmiske mikrobølgebaggrundsstråling. De relativistiske korrektioner kan dog ikke forklare selve eksistensen af Λ. Jeg vil i nogle kommende indlæg forsøge at forklare den fysiske baggrund for effekten.
Bjarne- Super Nova
Den moderne kosmologiske standardmodel er baseret på forskellige fysiske begreber, som er blevet tilføjet i årenes løb. Udgangspunktet er Einsteins Generelle Relativitetsteori (GR). Universet er ifølge GR en rumtid med afstande, som er koordinatuafhængige (invariante), på samme måde som en trekants størrelse er uafhængig af placeringen på et stykke milimeterpapir. Løsningen af Einsteins feltligninger for et generelt Univers er meget, meget kompliceret. Einsteins efterfølgere indførte derfor det kosmologiske princip. Alene navnet antyder, at der er tale om en filosofisk antagelse. Man anvender det kopernikanske princip på Universet. Man antager, at rumtiden kan opsplittes i en kosmisk tid og et tredimensionalt rum. Massefordelingen antages at være homogen (overalt den samme) og ekspansionen antages overalt at være isotrop (den samme i alle retninger). Einsteins feltligninger for et sådant univers blev løst af Alexander Friedmann, Georges Lemaître, Howard P. Robertson og Arthur Geoffrey Walker (FLRW):
Friedmann–Lemaître–Robertson–Walker (FLRW)
Den mest generelle løsning inkluderer Einsteins kosmologiske konstant Λ. Et tomt univers svarer til rumtiden for et de Sitter univers, som har en konstant rumtidskrumning. Λ = 0 svaret til den specielle relativitetsteoris rumtid. Einstein og de Sitter blev i 1932 enige om for altid at begrave Λ, dvs sætte Λ = 0. Begrundelsen var, at den ikke mere var nødvendig (Einsteins statiske univers var blevet modbevist af Hubble). Det fysiske samfund godtog argumentet, hvorimod astronomerne var mere skeptiske (de var bekymrede over en modstrid mellem Universets alder og Jordens alder).
Bjarne- Super Nova
Det blev hurtigt klart, at FLRW modellen for et massedomineret univers er identisk med den newtonske løsning for en opadrettet radial bevægelse. Enten er hastigheden over undvigelseshastigheden, og rummet ekspanderer for evigt, eller hastigheden er under undvigelseshastigheden, og rummet når en maksimal størrelse, hvorefter det trækker sig sammen. Der er en sammenhæng mellem de to tilfælde og rummets krumning. Det evigt ekspanderende rum har en negativ krumning, hvorimod del kollapsende rum har en positiv krumning. Hvis massetætheden har en speciel kritisk værdi, vil rummets ekspansion langsomt gå i stå, og rummets krumning er nul, dvs det er fladt.
Bjarne- Super Nova
Hvis en FLRW model starter med et fladt rum, vil rummet for altid forblive fladt. Nu er sådanne katagoriske påstande sjældent helt så uproblematiske, som man i første omgang tror. Lad mig anvende den newtonske model til at illustrere problemet. Jeg vil betragte en kugleskal r, som indeholde den konstante masse M. Jeg betragter den specifikke (per masse) energi, K, for et legeme på kugleskallen. Denne er givet ved energiligningen:
(1/2)(dr/dt)2 – GM/r = K
hvor G er gravitationskonstanten. Jeg ganger ligningen med 2 og finder
(dr/dt)2 = 2GM/r + 2K
Massen inden for kugleskallen er givet M = (4π/3)r3ρ, hvor ρ er massetætheden. Denne indsættes i energiligningen, og jeg dividerer med r2. Jeg definerer desuden hubble-funktionen: H(t) = (dr/dt)/r. Resultatet bliver Friedmanns ligning:
H2 = (8π/3)Gρ + 2K/r2
Den kritiske tæthed ρc fås ved at sætte K = 0, så den er defineret ved
H2 = (8π/3)ρc
Jeg definerer dernæst tæthedsfunktionen: Ω(t) = ρ/ρc, så Friedmanns ligning antager formen:
H2 = ΩH2 + 2K/r2
Jeg dividerer med H2 og finder Ω:
Ω = 1 – 2K/(rH)2 = 1 – 2K/(dr/dt)2
Denne plus energiligningen anvendes til at finde: (1 – 1/Ω)/r = konstant. Konstanten kan findes for en bestemt radius r0, så den endelige ligning bliver:
(1 – 1/Ω) = (1 – 1/Ω0)(r/r0)
Bjarne- Super Nova
Denne her ligning (1 – 1/Ω) = (1 – 1/Ω0)(r/r0) viser, at Ω nærmig sig 1, når r nærmer sig 0. Eller sagt på en anden måde: Ω fjerner sig fra 1, når r vokser. Husk, at Ω er tætheden divideret med den kritiske tæthed. Modellen fjerner sig fra den kritiske tæthed, når rummet ekspanderer. Rummet forbliver kun fladt, hvis det startede med at være eksakt fladt, dvs Ω = 1. En lille afvigelse kan få rummet til at kollapse, inden det når den nuværende størrelse, eller det kan ekspandere så hurtigt, at der ikke dannes galakser. Dette er det berømte flatness problem, dvs fladhedsproblemet.
Løsningen blev fundet i begyndelsen af 1980’erne i form af et inflationsfelt φ med en tilhørende energitæthed V(φ), som får rummet til at ekspandere eksponentielt i en tilstrækkelig lang tid til at fjerne alle ujævnheder; inflationen virker som et kosmisk strygejern. Dette er grunden til, at man forventer, at rummet er fladt.
Bjarne- Super Nova
Men så er en flad FLRW model den helt rigtige beskrivelse af Universet? Ikke så hurtig: Inflationsfeltet er ikke et klassisk felt, men i stedet et fluktuerende kvantefelt. Når inflationsfeltets energi ved slutningen af inflationsfasen omsættes til strålingsenergi, vil der være små fluktuationer i energitætheden. Når vi når frem til et stykke tid før den elektromagnetiske stråling frigøres fra spredning på elektroner, består stoffet af He-kerner, protoner, elektroner og neutrinoer. Stoffet består af et plasma, hvor tæthedsfluktuationerne er blevet til stående lydbølger med en karakteristisk fysisk størrelse svarende til det stykke, som lydbølgerne har bevæget sig siden begyndelsen. Denne længde kaldes lydhorisonten. Strålingen afkobles fra elektronerne meget på samme måde, som strålingen forlader Solens fotosfære. Man kan beregne fluktuationernes størrelse, hvis de skal kunne nå at danne galakser. Dette blev allerede gjort i 1970’erne ved anvendelse af en flad FLRW-model uden kosmologisk konstant. Beregningerne viste, at de sagtens burde kunne måles. Der blev foretaget mange forsøg på at måle fluktuationerne op gennem 1970’erne, men uden held. Noget var tilsyneladende helt galt, fluktuationerne var meget mindre end forudset. På samme tid fandt man, at spiralgalakserne havde flade rotationskurver langt uden for den synlige del af galaksen. Noget tydede på, at Universet var fyldt med mørkt stof. Ploblemet med Universets plasmafase er, at den ikke tillader vækst af tæthedsfluktuationerne, da atomkernerne er koblet til strålingen via elektronerne. Det samme gælder ikke det mørke stof. Fluktuationer i mørkt stof kan godt vokse, da partiklerne ikke vekselvirker med strålingen. Det viste sig, at koldt mørk stof (CDM = Cold Dark Matter) kan forklare den lave amplitude for temperaturfluktuationerne. De store tæthedsfluktuationer findes i virkelighede i det mørke stof, som man ikke kan måle.
Sådan blev CDM-modellerne født. Temperaturfluktuationerne blev første gang målt med COBE-satellitten i 1992, men den kunne ikke måle lydhorisontens vinkelstørrelse på himmelkuglen.
Bjarne- Super Nova
Der hændte 2 ting op gennem 1990’erne: a) man forsøgte en gang for alle at vise, om rummet var fladt ved anvendelse at supernovaer af type Ia som standardlyskilde. b) HST skulle en gang for alle bestemme værdien af hubble-konstante.
Den nye og bedre bestemte H0 viste uheldigvis, at et fladt univers er signifikant yngre end de ældste stjerner.
Supernova målingerne var en stor overraskelse. De kunne kun forklares, hvis Universet accelererer i stedet for at decelerere, som man havde ventet.
Man måtte grave Einsteins kosmologiske konstant op af graven for at forklare observationerne. Den nye ΛCDM-model kunne både forklare supernovaobservationerne og en alder for Universet, som er i overensstemmelse med aldrene for de ældste stjerner.
WMAP-satellitten blev opsendt i 2001, og den fungerede frem til 2010. Formålet var at måle power spektret for temperaturfluktuationerne, så man herudfra kunne finde den bedste kosmologiske FLRW-model for Universet. Den bedste model var den flade ΛCDM-model.
ESA’s Planck satellit blev opsendt i 2009, og den fungerede frem til 2013. Den bestemte parametrene for ΛCDM med hidtil uhørt nøjagtighed. Den kunne således også finde en meget nøjagtig værdi for H0 ud fra lydhorisontens størrelse på himmelkuglen. Her begynder så problemet, som artiklen omhandler.
Bjarne- Super Nova
Planck-konsortiets bedste værdi for hubble-konstanten er H0 = 67.81±0.92 km/s/Mpc.
Riess et al.’s seneste bestemmelse af den lokale hubble-konstant er derimod H0 = 73.24±1.74 km/s/Mpc.
Begge bestemmelser anvender ΛCDM-modellen, som igen er en FLRW-model baseret på det kosmologiske princip.
Nu behøver man jo bare kaste et blik på himlen for at konkludere, at det nære univers hverken er homogent eller isotropt. Krzysztof Bolejkos hovedargument er, at den rumlige massefordeling seriøst begyndte at afvige fra det kosmologiske princip ca. en milliard år efter Universets start. Undertætte områder har lokalt en negativ krumning og ekspanderer hurtigere end FLRW-modellen. Overtætte områder har derimod en positiv krumning, så de ekspanderer langsommere end FLRW-modellen. Resultatet er store undertætte områder omgivet af lange filamenter af overtætte områder, hvor de første galakser dannes.
Den observerede rumvinkel af et fjernt objekt forstørres af den massetæthed, som strålerne passerer på deres vej mod observatøren. Fladelysstyrken af et objekt med en bestemt rødforskydning ændres ikke undervejs mod observatøren. Den observerede flux fra en supernova bliver derfor proportional med forstørrelsen. Da de undertætte områder fylder et langt større rumfang end de overtætte områder, vil langt de fleste supernovaers flux blive svækket i forhold til en FLRW-model. En svækkelse af fluxen svarer til et rum med en effektiv negativ krumning. Bolejko kan således forklare forskellen mellem de to værdier af H0. Forskellen skyldes, at det kosmologiske princip bryder sammen.
- Emnet 'Kan en opdukkende rumlig krumning forklare den lokale H0?' er lukket for nye svar.